Crémieux@cremieuxrecueil• almost 2 years ago

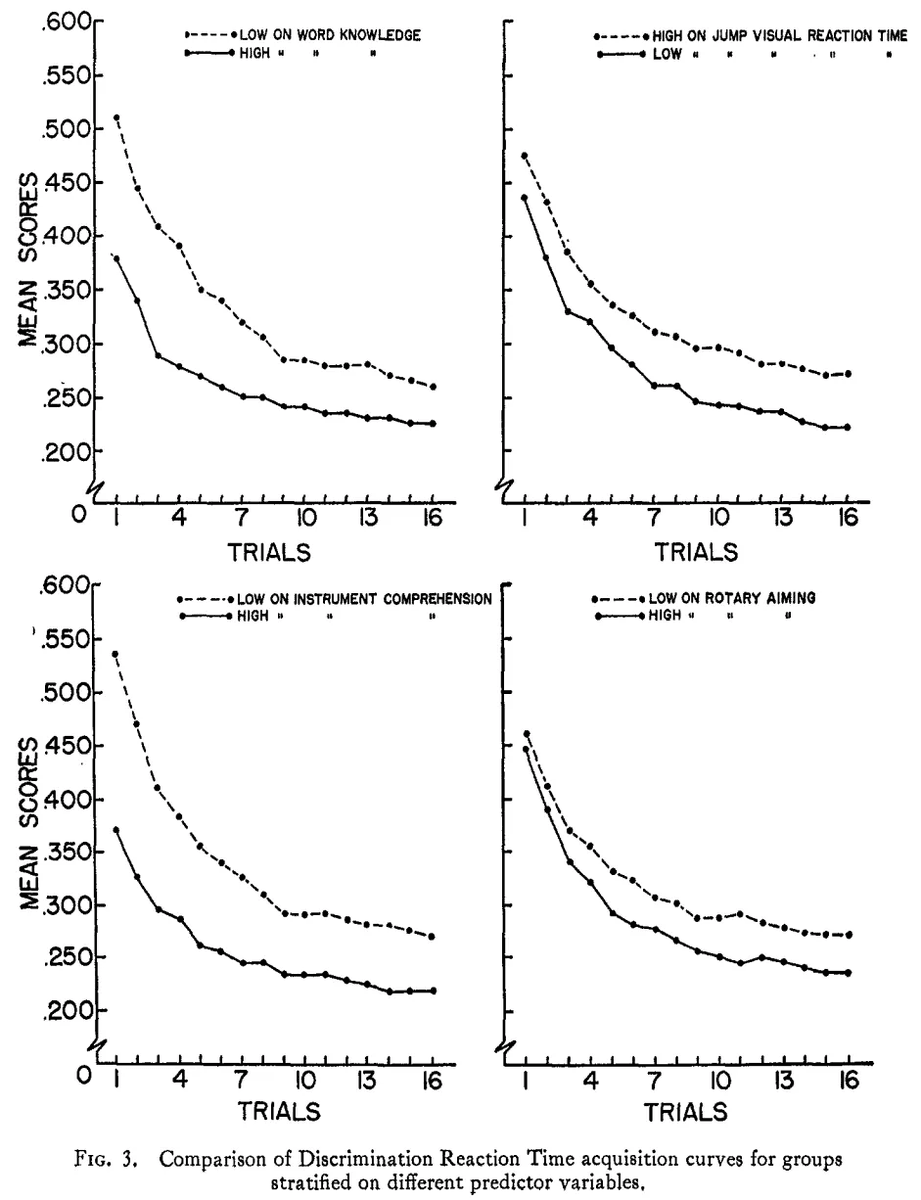
This is one of those studies where the interpretation reveals a lot about the person doing the interpreting, while the study itself reveals basically nothing. There are no discrete units of learning, so when someone says that students at different levels of ability learn at similar rates because they get between, say, 0.5 and 1.5% better at a task each time they do it and thus learning rates barely matter, they're revealing that they just don't care about being right. If a person gets 1.5% better at a task each time they do it and another person gets 0.5% with each iteration, are they learning at a remarkably similar rate? The answer is "yes", only if you think you have a reference point for learning rates that makes 'just 1%' meaningful. But you don't, because no one does. All we have is the relative learning rates, and we know that the person getting 1.5% better at a task each time is learning three times faster than the person getting 0.5% better. That 1% difference is suddenly enormous, because, well it is enormous. But this study doesn't really tell us very much even beyond this issue, because it suffers from two more problems: regression to the mean and range restriction. The tasks used in this study have capped scoring. For students near the score limits, they will apparently not learn anything because there's less room for them to improve, and more room for error to determine their scores in any given performance iteration. Is it correct to say that students with higher initial scores are slow learners? One of the ways you can see this is to stratify learning rates by initial knowledge. Those at the 25th percentile took 13.13 iterations to reach 80% mastery of their material, with an initial mean of 55.21%; those at the median took 6.54 iterations to reach 80% mastery with an initial mean of 66.05%; those at the 75th percentile took 3.66 iterations to reach 80% mastery with an initial mean of 75.17%. Accordingly, the learning rates per iteration were 1.89%, 2.13%, and 1.32%. And this makes sense! The median group was the least restricted, the top-performing group was the most restricted, and the bottom group was brought up by regression to the mean (RttM). RttM is why the top group also appeared to learn so slowly. Some of them were initial high-scorers who were anomalously high-scorers, so we should expect their scores to relatively decrease, pulling them further from 80% mastery of the material even as they learn. On the other hand, the lowest performers ought to move up more because of the anomalously low-performing among them, even if they're not especially fast at learning. If you stratify the groups by their learning rates, the 75th percentile was 51% faster than the 25th percentile, whereas the median was 32% faster than the 25th percentile and the 75th percentile outpaced the median by 14%. But more importantly, we get to see that what the study calls "learning rates" are just a reflection of initially poor scoring and having a correspondingly greater room to advance. The 25th percentile of learners (by rate) initially had 58.45% mastery, followed by the median who had 49.05% mastery, and then by the 75th percentile, who only had 43.11% mastery. These results are dominated by artefacts, and downloading the data to correct it actually makes that very clear when you go in with this perspective in mind. To put this differently, consider speed. Speed is objective, so it makes things clearer. Over many trials, the initially smartest people end up faster than the initially least intelligent people. They also reach their training asymptote earlier, which makes sense, because they are faster learners. But if you took the raw percentage improvements over arbitrarily-many trials, this fact would eventually mislead you about the "speed learning" of the smartest people, because their average improvement would diminish as the number of trials increases, relative to individuals who started off slower and reached their asymptote later. Over a long enough series of trials, the difference would, of course, diminish. If you set a mean score to be achieved and this was sufficiently below even the smarter group's initial performance, then you would find the same thing as in the OP paper. This can be absurd, as in the window where groups are stratified by instrument comprehension. Imagine the low-performers (initial score ~540) and the high-performers (initial score ~375) both had to reach a score of 350. The high-performers do it in two trials. Their learning rate is thus (375-350)/2 = 12.5. The learning rate for the low-performers is (540-350)/5-6 (we'll go with 6), giving them a learning rate that's apparently 287% as fast as the high-performers. The initially low-performs are also disproportionately people who have trouble initially grasping how things work. So even if there was a common metric - say, improving your score by 100 - it might not be comparable, because -100 from a baseline of 540 may not be the same as -100 from a baseline of 375, because the people with the baseline of 375 don't have the additional variance implied by "not getting the rules". This also provides us with another critical piece of information: people have different limits, even if they can learn at similar enough rates on some metric. If we set the desired level of performance to, say, a mean score of 250, then the lower-performing group might never be able to reach it, regardless of their initially higher apparent learning rates. Their asymptote is just considerably higher than this level of speed; learning faster or not, they're not ever going to reach the level the initial high-performers get to. There are people who learn relatively quickly and those who learn relatively slowly. There's more than a century of research into this subject and the success of gifted education programs speaks volumes about their reality. There's no need to be fooled into thinking otherwise by an analysis that conceptualizes learning rates in an unintuitive way and which doesn't even begin to seriously investigate the subject. Let's stay serious. Sources: https://t.co/gF7MoQ4eqx https://t.co/adxwwdExBR