🧵 View Thread
🧵 Thread (18 tweets)

I feel this way about a lot of things. Even teaching math in schools... it makes sense to teach the history of math. The drama, the tension, *dramatic pause* the tea https://t.co/5pDuz7XumO

Suddenly felt this strong urge to become a schoolteacher https://t.co/b9GAz694le


Shall we? Let’s do this! What is trigonometry? Trigonometry begins with the cult of Triangle worship Would you like the secrets of the universe? You must recite the Pythagorean prayer before you may obtain it. Recite it!!! [Mr. Visa gets dragged out of class by security] https://t.co/StXfcXRzuo

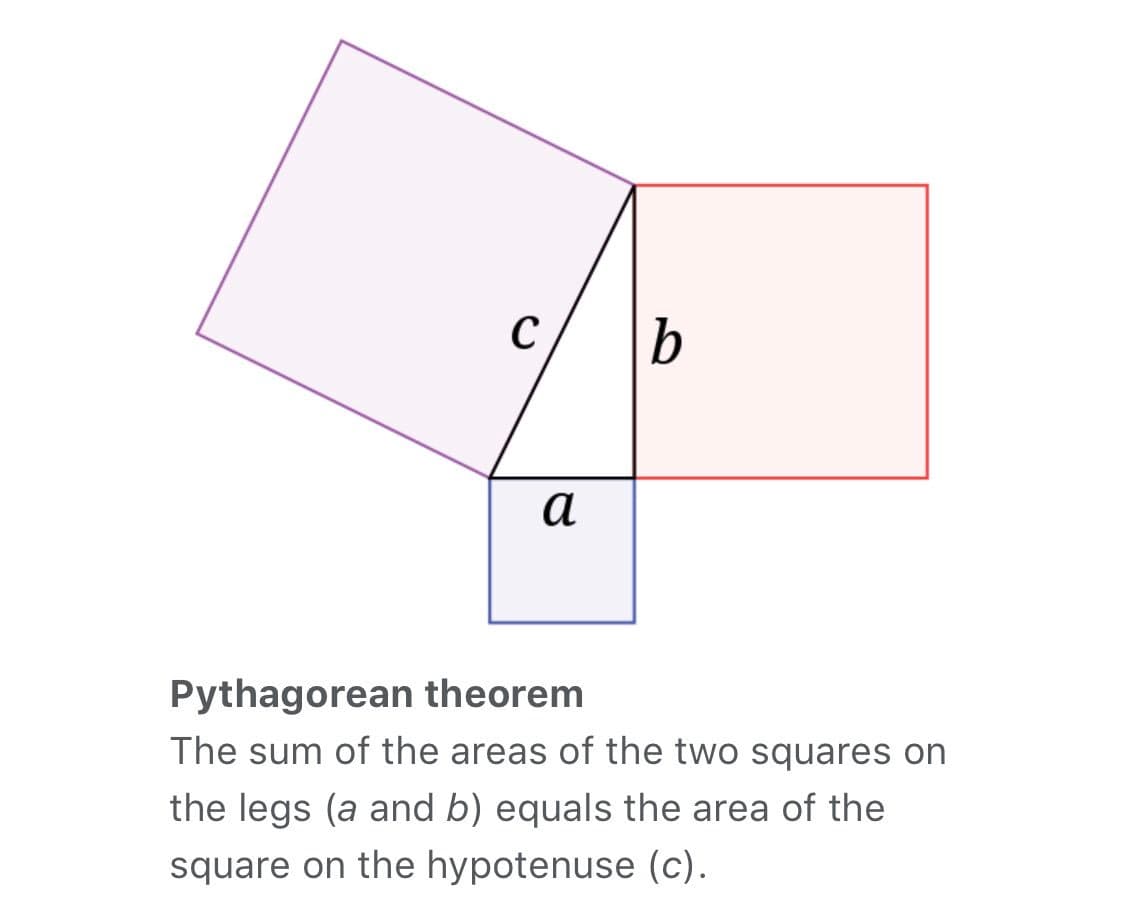
Pythagoras’s theorem - he might not have been the first to discover it, but he was the first popular kid to get all the retweets - proved that there’s a relationship between the lengths of a right angled triangle This shit is *wild!*. It always works, and nobody really knows why https://t.co/JaaaMDfiMp

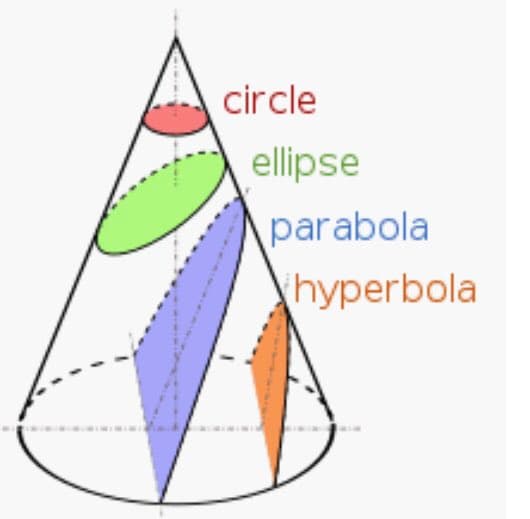
Ok but so what? Why should anybody care about right angled triangles? Expand your minds, kids. It’s not just “about triangles”. It’s about ratios & lengths. Trigonometry allows you to *know the unknown*. Unknown heights, unknown lengths. Because the universe just be like that https://t.co/3LFHmkjvzH


Idk if your minds are ready for this but I’m here to inform you that Shit Gets WILDER. See, the magic of right-angle triangles isn’t just in lengths. It’s also in *angles*. It’s all connected! Just stare at this for a minute even if you don’t understand it https://t.co/8KBnkT7tAg

Trig isn’t abt passing tests. Nobody worshipped triangles for that. It’s to discover the insane truth that the universe is, to some degree, knowable. And there are things you can know just by *thinking*!! You just need to learn the r/ships between things https://t.co/aKOFjwNVBM

Imagine what it must’ve been like to figure out the circumference of the earth - ~40,000 kilometres - over 2,000 years ago! No rockets, no GPS, nothing - Eratosthenes figured it out with math, and thinking. Can you feel the *power* in that? What a legacy https://t.co/QOQaBi7nFo

[pounds table] learning, *true* learning, is the most radical punk-ass shit. School wants you to be a pocket lighter - a small, predictable flame that does what it’s told & doesn’t ask too many questions. I want y’all to be f***in’ firestorms. Ignite the eons with your curiosity https://t.co/vNe5qVWnv4


The ratio of any circle’s circumference to its diameter is a constant. We call it pi. This simple relationship has *captivated* mathematicians for thousands of years. You can spend a lifetime exploring this. And as we saw in the unit circle earlier, ~it’s all connected~ https://t.co/n8ZMRrSIlT


”Why are there four seasons in a year? Because daylight follows an approximate sine wave, and it and its derivative have 4 maxima and minima” - @stevenstrogatz https://t.co/NOa5EyIhqt

This rabbit changes color for camouflage when the seasons change - and it does this by being sensitive to the amount of daylight each day (which follows abovementioned sine curve) https://t.co/ruLP5YuT61

Cute & cool: the snowshoe hare changes colours for camouflage. But it doesn’t know what month it is - it relies on a circadian timer to keep track of the daylight:darkness ratio. If you blindfold it in July (omg 😂) it starts changing color earlier 😭❤️ https://t.co/d6nDaHTv2I https://t.co/NeIbHB19Vx


c o n g r u e n t t r i a n g l e s https://t.co/bVxSGh0CRI

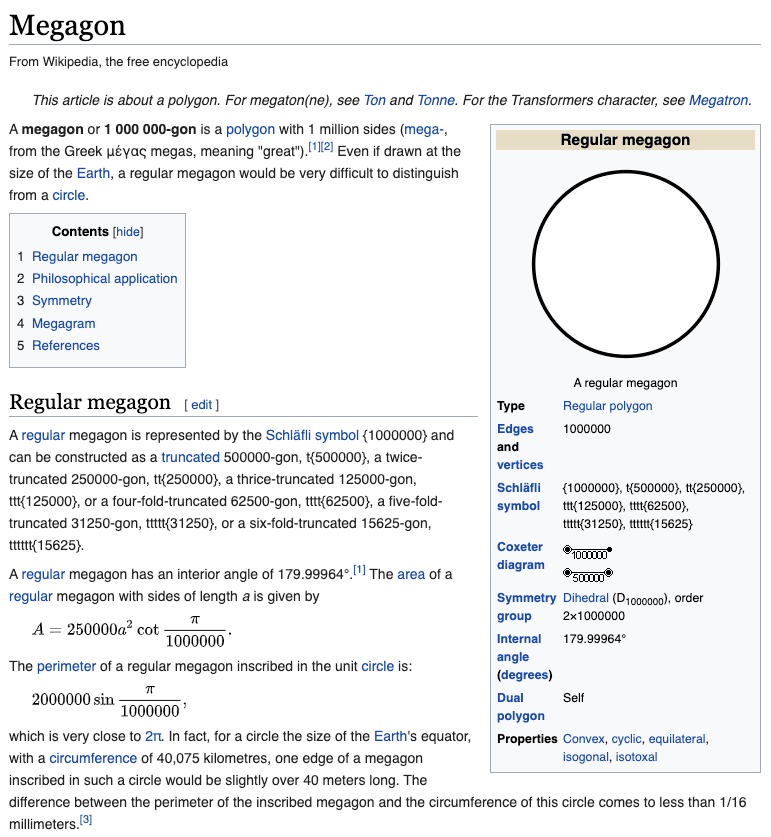
A megagon is a polygon (...a shape) with a million sides. Even if it were as large as the Earth, it would be effectively impossible for humans to distinguish it from a circle. Which makes it a simple, potent example of a well-defined concept that cannot be visualized. https://t.co/8yxAW2hQKo

calculus is the study of rate of change, ie change over time. the derivative is the *instantaneous* rate of change at a specific point, aka the slope of the tangent line to the graph of the function f(x) https://t.co/Vme680PkGM


this is how you do it https://t.co/7bJs2DHxk8